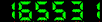Complex variables and applications / (Record no. 1113)
[ view plain ]
| 000 -LEADER | |
|---|---|
| fixed length control field | 05024cam a22002534a 4500 |
| 001 - CONTROL NUMBER | |
| control field | 143 |
| 005 - DATE AND TIME OF LATEST TRANSACTION | |
| control field | 20200820104506.0 |
| 008 - FIXED-LENGTH DATA ELEMENTS--GENERAL INFORMATION | |
| fixed length control field | 021108s2004 iaua b 001 0 eng |
| 020 ## - INTERNATIONAL STANDARD BOOK NUMBER | |
| International Standard Book Number | 0072872527 (alk. paper) |
| 020 ## - INTERNATIONAL STANDARD BOOK NUMBER | |
| International Standard Book Number | 9780072872521 |
| 040 ## - CATALOGING SOURCE | |
| Transcribing agency | DLC |
| 082 00 - DEWEY DECIMAL CLASSIFICATION NUMBER | |
| Classification number | 515.9 |
| Edition number | 21 |
| Item number | B87717 |
| 100 1# - MAIN ENTRY--PERSONAL NAME | |
| Personal name | Brown, James Ward. |
| 245 10 - TITLE STATEMENT | |
| Title | Complex variables and applications / |
| Statement of responsibility, etc | James Ward Brown, Ruel V. Churchill. |
| 250 ## - EDITION STATEMENT | |
| Edition statement | 7th ed. |
| 260 ## - PUBLICATION, DISTRIBUTION, ETC. (IMPRINT) | |
| Place of publication, distribution, etc | Boston : |
| Name of publisher, distributor, etc | McGraw-Hill Higher Education, |
| Date of publication, distribution, etc | 2004. |
| 300 ## - PHYSICAL DESCRIPTION | |
| Extent | xvi, 458 p. |
| Other physical details | ill. ; |
| Dimensions | 25 cm. |
| 490 1# - SERIES STATEMENT | |
| Series statement | Brown-Churchill series |
| 500 ## - GENERAL NOTE | |
| General note | Includes bibliographical references (p. 437-439) and index. |
| 650 #0 - SUBJECT ADDED ENTRY--TOPICAL TERM | |
| Topical term or geographic name as entry element | Functions of complex variables. |
| 700 1# - ADDED ENTRY--PERSONAL NAME | |
| Personal name | Churchill, Ruel V. |
| 942 ## - ADDED ENTRY ELEMENTS (KOHA) | |
| Koha item type | Books |
| 505 0# - FORMATTED CONTENTS NOTE | |
| Formatted contents note | 1. 1 complex numbers<br/>2. Sums and products<br/>3. Basic algebraic properties<br/>4. Further properties<br/>5. Moduli<br/>6. Complex conjugates<br/>7. Exponential form<br/>8. Products and quotients in exponential form<br/>9. Roots of complex numbers<br/>10. Examples<br/>11. Regions in the complex plane<br/>12. 2 analytic functions<br/>13. Functions of a complex variable<br/>14. Mappings<br/>15. Mappings by the exponential function<br/>16. Limits<br/>17. Theorems on limits<br/>18. Limits involving the point at infinity<br/>19. Continuity<br/>20. Derivatives<br/>21. Differentiation formulas<br/>22. Cauchy–riemann equations<br/>23. Sufficient conditions for differentiability<br/>24. Polar coordinates<br/>25. Analytic functions<br/>26. Examples<br/>27. Harmonic functions<br/>28. Uniquely determined analytic functions<br/>29. Reflection principle<br/>30. 3 elementary functions<br/>31. The exponential function<br/>32. The logarithmic function<br/>33. Branches and derivatives of logarithms<br/>34. Some identities involving logarithms<br/>35. Complex exponents<br/>36. Trigonometric functions<br/>37. Hyperbolic functions<br/>38. Inverse trigonometric and hyperbolic functions<br/>39. 4 integrals<br/>40. Derivatives of functions w(t)<br/>41. Definite integrals of functions w(t)<br/>42. Contours<br/>43. Contour integrals<br/>44. Examples<br/>45. Upper bounds for moduli of contour integrals<br/>46. Antiderivatives<br/>47. Examples<br/>48. Cauchy–goursat theorem<br/>49. Proof of the theorem<br/>50. Simply and multiply connected domains<br/>51. Cauchy integral formula<br/>52. Derivatives of analytic functions<br/>53. Liouville’s theorem and the fundamental theorem of algebra<br/>54. Maximum modulus principle<br/>55. 5 series<br/>56. Convergence of sequences<br/>57. Convergence of series<br/>58. Taylor series<br/>59. Examples<br/>60. Laurent series<br/>61. Examples<br/>62. Absolute and uniform convergence of power series<br/>63. Continuity of sums of power series<br/>64. Integration and differentiation of power series<br/>65. Uniqueness of series representations<br/>66. Multiplication and division of power series<br/>67. 6 residues and poles<br/>68. Residues<br/>69. Cauchy’s residue theorem<br/>70. Using a single residue<br/>71. The three types of isolated singular points<br/>72. Residues at poles<br/>73. Examples<br/>74. Zeros of analytic functions<br/>75. Zeros and poles<br/>76. Behavior of f near isolated singular points<br/>77. 7 applications of residues<br/>78. Evaluation of improper integrals<br/>79. Example<br/>80. Improper integrals from fourier analysis<br/>81. Jordan’s lemma<br/>82. Indented paths<br/>83. An indentation around a branch point<br/>84. Integration along a branch cut<br/>85. Definite integrals involving sines and cosines<br/>86. Argument principle<br/>87. Rouche;’s theorem<br/>88. Inverse laplace transforms<br/>89. Examples<br/>90. 8 mapping by elementary functions<br/>91. Linear transformations<br/>92. The transformation w = 1/z<br/>93. Mappings by 1/z<br/>94. Linear fractional transformations<br/>95. An implicit form<br/>96. Mappings of the upper half plane<br/>97. The transformation w = sin z<br/>98. Mappings by z2 and branches of z1/2<br/>99. Square roots of polynomials<br/>100. Riemann surfaces<br/>101. Surfaces for related functions<br/>102. 9 conformal mapping<br/>103. Preservation of angles<br/>104. Scale factors<br/>105. Local inverses<br/>106. Harmonic conjugates<br/>107. Transformations of harmonic functions<br/>108. Transformations of boundary conditions<br/>109. 10 applications of conformal mapping<br/>110. Steady temperatures<br/>111. Steady temperatures in a half plane<br/>112. A related problem<br/>113. Temperatures in a quadrant<br/>114. Electrostatic potential<br/>115. Potential in a cylindrical space<br/>116. Two-dimensional fluid flow<br/>117. The stream function<br/>118. Flows around a corner and around a cylinder<br/>119. 11 the schwarz–christoffel transformation<br/>120. Mapping the real axis onto a polygon<br/>121. Schwarz–christoffel transformation<br/>122. Triangles and rectangles<br/>123. Degenerate polygons<br/>124. Fluid flow in a channel through a slit<br/>125. Flow in a channel with an offset<br/>126. Electrostatic potential about an edge of a conducting plate<br/>127. 12 integral formulas of the poisson type<br/>128. Poisson integral formula<br/>129. Dirichlet problem for a disk<br/>130. Related boundary value problems<br/>131. Schwarz integral formula<br/>132. Dirichlet problem for a half plane<br/>133. Neumann problems<br/>134. Appendixes<br/>135. Bibliography<br/>136. Table of transformations of regions<br/>137. Index<br/> |
| Withdrawn status | Damaged status | Not for loan | Home library | Current library | Date acquired | Full call number | Barcode | Date last seen | Price effective from | Koha item type |
|---|---|---|---|---|---|---|---|---|---|---|
| UE-Central Library | UE-Central Library | 29.06.2018 | 515.9 B87717 | T143 | 28.02.2020 | 29.06.2018 | Books |